ballsjae.blogg.se - Shapiro wilk test

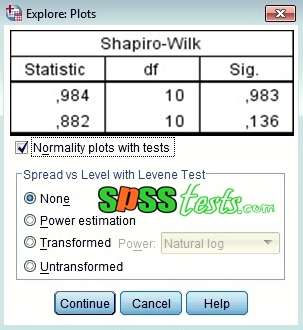
StatsDirect requires a random sample of between 3 and 2,000 for the Shapiro-Wilk test, or between 5 and 5,000 for the Shapiro-Francia test. The two other tests are semi-parametric analyses of variance: Shapiro-Wilk W ( Conover, 1999 Shapiro and Wilk, 1965 Royston, 1982a, 1982b, 1991a, 1995) and Shapiro-Francia W' ( Shapiro and Francia, 1972 Royston 1983). You might wish to clean your dataset carefully before exploring its distribution in this way.

These tests are calculated using moments about the mean, therefore they are quite sensitive to outliers. The test of skewness focuses on the symmetry of the distribution the test of kurtosis examines it's peakedness and the omnibus chi-square (or k-square) test combines these characteristics ( D'Agostino et al., 1990). The common hypothesis is that the sample has been drawn at random from a normal distribution. This function enables you to explore the distribution of a sample and test for certain patterns of non-normality.Ī normal probability plot is provided, after some basic descriptive statistics and five hypothesis tests. If the test statistic W is smaller than the critical threshold (see table below) the assumption of a normal distribution has to be rejected.Menu location: Analysis_Parametric_Normality.

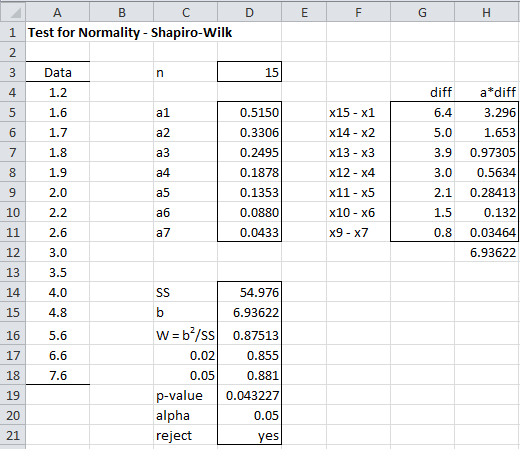
Calculate the test statistic W = b 2/S 2.

The parameters a n-i+1 depend on the sample size and have to be taken from a table published by Shapiro and Wilk

a) if n is even, then b is calculated using mit k = n/2:ī) if n is odd, b is calculated by using k=(n-1)/2, the median must not be included.

The sample of size n (x 1,x 2.x n) has to be sorted in increasing order, the resulting sorted sample will be designated by y 1,y 2.y n (y 1 < y 2 <.

In order to calculate the statistic W one has to perform the following procedure: If the quotient is significantly lower than 1.0 then the null hypothesis (of having a normal distribution) should be rejected. Both estimated values should approximately equal in the case of a normal distribution and thus should result in a quotient of close to 1.0. The basis idea behind the Shapiro-Wilk test is to estimate the variance of the sample in two ways: (1) the regression line in the QQ-Plot allows to estimate the variance, and (2) the variance of the sample can also be regarded as an estimator of the population variance. In contrast to other comparison tests the Shapiro-Wilk test is only applicable to check for normality. The Shapiro-Wilk test is a test for normal distribution exhibiting high power, leading to good results even with a small number of observations.